How To Find Height Of Parallelogram With Sides

1.2.2: Bases and Heights of Parallelograms

1. Last updated

2. Save equally PDF

Page ID

39636

Lesson

Let'due south investigate the surface area of parallelograms some more.

Exercise \(\PageIndex{1}\): A Parallelogram and Its Rectangles

Elena and Tyler were finding the surface area of this parallelogram:

Figure \(\PageIndex{1}\)

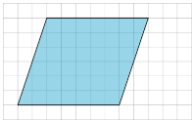
Move the slider to see how Tyler did information technology:

Move the slider to run into how Elena did information technology:

How are the 2 strategies for finding the expanse of a parallelogram the same? How they are dissimilar?

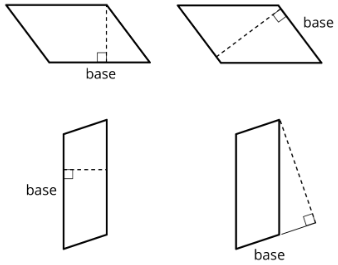
Exercise \(\PageIndex{2}\): The Correct Top?

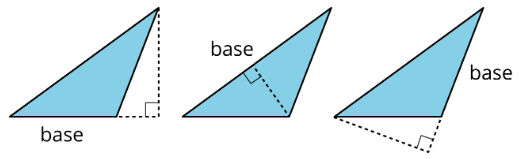
Study the examples and non-examples of bases and heights of parallelograms.

• Examples: The dashed segments in these drawings represent the corresponding height for the given base.

Effigy \(\PageIndex{2}\)

• Non-examples: The dashed segments in these drawings do not represent the corresponding height for the given base.

Figure \(\PageIndex{three}\)

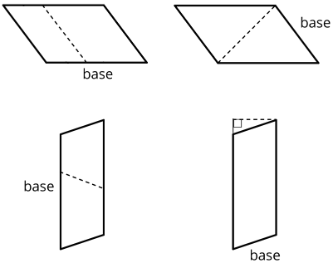
1. Select all the statements that are true about bases and heights in a parallelogram.
   1. Only a horizontal side of a parallelogram can be a base of operations.
   2. Any side of a parallelogram can exist a base.
   3. A height can be drawn at any angle to the side chosen every bit the base.
   4. A base and its corresponding height must exist perpendicular to each other.
   5. A peak can only be fatigued inside a parallelogram.
   6. A pinnacle can be drawn outside of the parallelogram, as long as it is drawn at a 90-degree angle to the base.
   7. A base of operations cannot be extended to encounter a height.
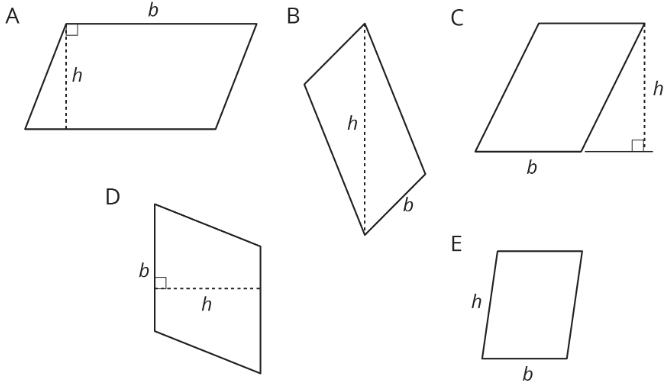
2. Five students labeled a base \(b\) and a corresponding height \(h\) for each of these parallelograms. Are all drawings correctly labeled? Explain how yous know.

Effigy \(\PageIndex{iv}\)

Are you ready for more?

In the applet, the parallelogram is made of solid line segments, and the pinnacle and supporting lines are made of dashed line segments. A base b and corresponding height h are labeled.

Do \(\PageIndex{3}\): Finding the Formula for Expanse of Parallelograms

For each parallelogram:

• Identify a base and a corresponding height, and record their lengths in the table.
• Discover the area of the parallelogram and tape it in the last column of the table.

Figure \(\PageIndex{5}\)

Table \(\PageIndex{1}\)

parallelogram	base (units)	elevation (units)	area (sq units)
A
B
C
D
any parallelogram	\(b\)	\(h\)

In the concluding row, write an expression for the area of any parallelogram, using \(b\) and \(h\).

Are you ready for more than?

1. What happens to the area of a parallelogram if the height doubles but the base is unchanged? If the acme triples? If the height is 100 times the original?
2. What happens to the surface area if both the base and the acme double? Both triple? Both are 100 times their original lengths?

Summary

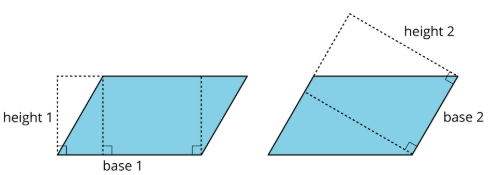
• Nosotros can cull any of the four sides of a parallelogram as the base. Both the side (the segment) and its length (the measurement) are called the base.
• If we describe any perpendicular segment from a point on the base to the opposite side of the parallelogram, that segment will always take the aforementioned length. We telephone call that value the height. In that location are infinitely many segments that can represent the height!

Figure \(\PageIndex{6}\): two copies of the same parallelogram. On the left, base = half-dozen units. Corresponding summit = iv units. On the right, base of operations = v units. Corresponding summit = 4.eight units. For both, iii unlike segments are shown to represent the superlative.

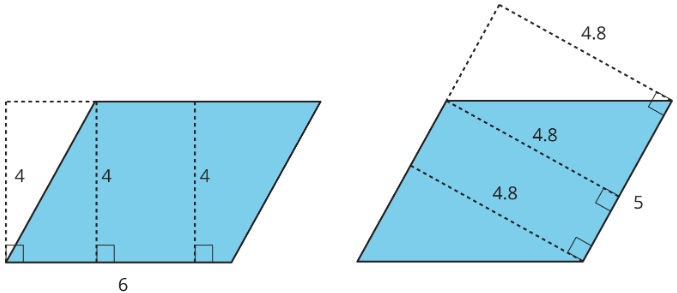
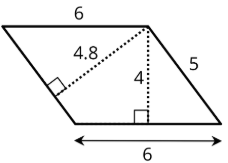
Here are two copies of the aforementioned parallelogram. On the left, the side that is the base is half-dozen units long. Its corresponding summit is 4 units. On the correct, the side that is the base is 5 units long. Its corresponding height is 4.8 units. For both, three different segments are shown to stand for the superlative. We could draw in many more!

No affair which side is chosen as the base, the area of the parallelogram is the product of that base and its corresponding height. We can check this:

\(4\times 6=24\qquad\text{ and }\qquad iv.viii\times 5=24\)

We tin can meet why this is true by decomposing and rearranging the parallelograms into rectangles.

Figure \(\PageIndex{7}\)

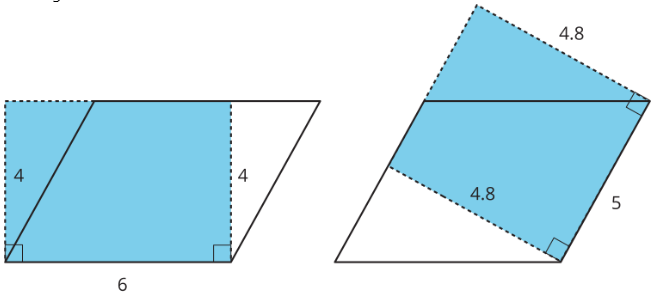
Discover that the side lengths of each rectangle are the base and height of the parallelogram. Even though the two rectangles have different side lengths, the products of the side lengths are equal, so they take the same area! And both rectangles have the same surface area every bit the parallelogram.

Nosotros oft apply letters to stand for numbers. If \(b\) is base of a parallelogram (in units), and \(h\) is the corresponding height (in units), then the surface area of the parallelogram (in square units) is the product of these two numbers. \(b\cdot h\)

Notice that we write the multiplication symbol with a small dot instead of a \(\times\) symbol. This is and then that nosotros don't get confused about whether \(\times\) means multiply, or whether the letter \(10\) is standing in for a number.

In high school, you will exist able to prove that a perpendicular segment from a point on one side of a parallelogram to the opposite side will always have the same length.

Figure \(\PageIndex{8}\)

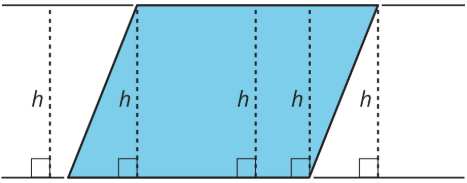
Y'all tin see this most easily when you draw a parallelogram on graph newspaper. For now, nosotros will merely use this as a fact.

Glossary Entries

Definition: base (of a parallelogram or triangle)

We can choose any side of a parallelogram or triangle to be the shape'due south base of operations. Sometimes we apply the word base to refer to the length of this side.

Effigy \(\PageIndex{9}\)

Definition: top (of a parallelogram or triangle)

The height is the shortest distance from the base of operations of the shape to the opposite side (for a parallelogram) or contrary vertex (for a triangle).

We tin prove the height in more than one identify, but it will always be perpendicular to the chosen base.

Figure \(\PageIndex{10}\)

Definition: Parallelogram

A parallelogram is a type of quadrilateral that has two pairs of parallel sides.

Here are ii examples of parallelograms.

Figure \(\PageIndex{11}\): 2 parallelograms with the angles and side lengths provided. On the left, Top and bottom sides = 5 units. Left and right sides = 4.24 units. Top left and lesser right angles = 135 degrees. Summit right and lesser left angles = 45 degrees. On the right, Top and lesser sides = ix.34 units. Left and right sides = iv units. Top left and bottom right angles = 27.2 degrees. Top correct and bottom left angles = 152.8 degrees.

Definition: Quadrilateral

A quadrilateral is a type of polygon that has 4 sides. A rectangle is an example of a quadrilateral. A pentagon is not a quadrilateral, because it has 5 sides.

Practice

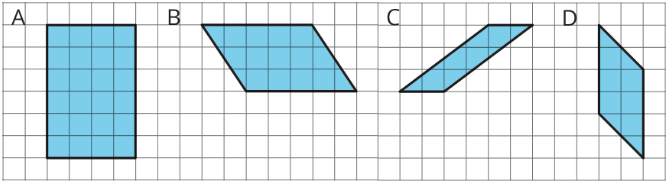
Exercise \(\PageIndex{4}\)

Select all parallelograms that have a right height labeled for the given base of operations.

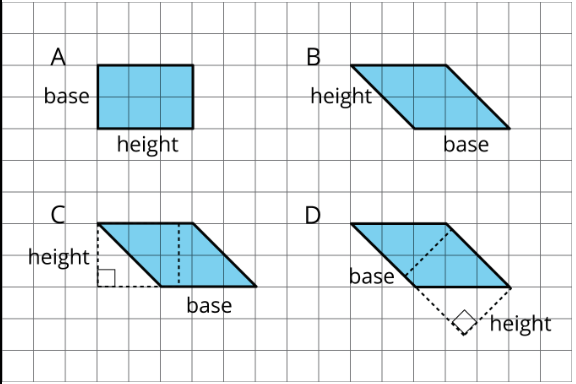
Figure \(\PageIndex{12}\): 4 parallelograms on a grid, labeled A, B, C, D. Parallelogram A, base = iii units, height = two units. Parallelogram B, base = 3 units, elevation = 2 units. Parallelogram C, base = 3 units, height = 2 units. Parallelogram D, base = diagonal across two unit squares, peak = three units.

1. A
2. B
3. C
4. D

Exercise \(\PageIndex{5}\)

The side labeled \(b\) has been chosen as the base for this parallelogram.

Figure \(\PageIndex{thirteen}\)

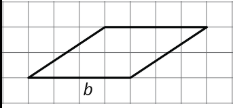
Draw a segment showing the height respective to that base of operations.

Exercise \(\PageIndex{6}\)

Detect the area of each parallelogram.

Figure \(\PageIndex{14}\): iii parallelograms on a filigree, labeled A, B, C. Parallelogram A, base = 4 units, top = 2 units. Parallelogram B, base = 5 units, height = 2 units. Parallelogram C, base of operations = 2 units, acme = 4 units.

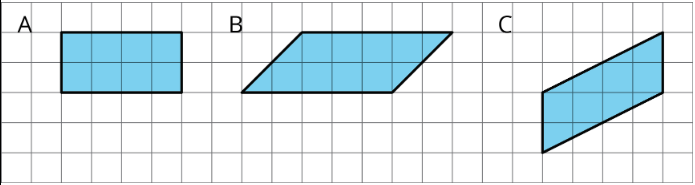
Practise \(\PageIndex{7}\)

If the side that is 6 units long is the base of operations of this parallelogram, what is its respective acme?

Figure \(\PageIndex{fifteen}\): A parallelogram with its lesser and top sides labeled 6 and its correct side labeled five. A dashed line perpendicular to the right side is labeled 4.8, and a dashed line perpendicular to the bottom side is labeled 4.

1. 6 units
2. iv.eight units
3. 4 units
4. 5 units

Exercise \(\PageIndex{viii}\)

Find the area of each parallelogram.

Figure \(\PageIndex{xvi}\): iii parallelograms labeled A, B, C. Parallelogram A, base of operations = 9 centimeters, height = 4 centimeters. Parallelogram B, base = 5 centimeters, summit = 4 centimeters. Parallelogram C, base = b, summit = h.

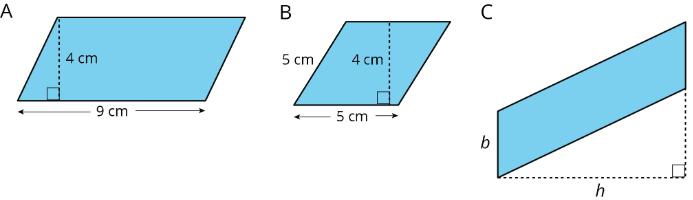
Practise \(\PageIndex{9}\)

Do you lot agree with each of these statements? Explicate your reasoning.

1. A parallelogram has six sides.
2. Opposite sides of a parallelogram are parallel.
3. A parallelogram can have i pair or two pairs of parallel sides.
4. All sides of a parallelogram have the aforementioned length.
5. All angles of a parallelogram accept the aforementioned mensurate.

(From Unit of measurement 1.two.1)

Exercise \(\PageIndex{10}\)

A square with an area of 1 square meter is decomposed into ix identical small squares. Each small-scale foursquare is decomposed into two identical triangles.

1. What is the expanse, in square meters, of 6 triangles? If you become stuck, consider drawing a diagram.
2. How many triangles are needed to compose a region that is \(one\frac{1}{2}\) square meters?

(From Unit of measurement 1.1.2)

Source: https://math.libretexts.org/Bookshelves/Arithmetic_and_Basic_Math/Book:_Basic_Math_%28Illustrative_Mathematics_-_Grade_6%29/01:_Area_and_Surface_Area/1.02:_Parallelograms/1.2.2:_Bases_and_Heights_of_Parallelograms

Posted by: gillespieextesed.blogspot.com

Share this post