How To Find X In Quadratic Equation
Quadratic Equations
85 Graphing Quadratic Equations
Learning Objectives
By the stop of this department, y'all will exist able to:
- Recognize the graph of a quadratic equation in two variables
- Observe the axis of symmetry and vertex of a parabola
- Find the intercepts of a parabola
- Graph quadratic equations in two variables
- Solve maximum and minimum applications
Recognize the Graph of a Quadratic Equation in 2 Variables
We have graphed equations of the grade ![]() . We called equations similar this linear equations because their graphs are straight lines.
. We called equations similar this linear equations because their graphs are straight lines.
Now, we volition graph equations of the form ![]() . We telephone call this kind of equation a quadratic equation in two variables.
. We telephone call this kind of equation a quadratic equation in two variables.
Quadratic Equation in Two Variables
A quadratic equation in 2 variables, where ![]() are real numbers and
are real numbers and ![]() , is an equation of the course
, is an equation of the course
![]()
Just similar we started graphing linear equations by plotting points, we will do the aforementioned for quadratic equations.
Let'due south look showtime at graphing the quadratic equation ![]() . Nosotros will choose integer values of
. Nosotros will choose integer values of ![]() betwixt
betwixt ![]() and two and detect their
and two and detect their ![]() values. Encounter (Effigy).
values. Encounter (Effigy).
| | |
| | |
| 0 | 0 |
| one | 1 |
| | i |
| 2 | 4 |
| | 4 |
Notice when we let ![]() and
and ![]() , we got the same value for
, we got the same value for ![]() .
.
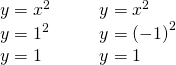
The aforementioned thing happened when we permit ![]() and
and ![]() .
.
At present, we will plot the points to testify the graph of ![]() . See (Figure).
. See (Figure).
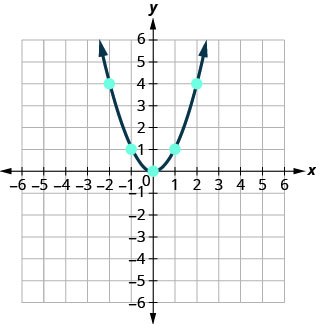
The graph is non a line. This figure is chosen a parabola. Every quadratic equation has a graph that looks like this.
In (Figure) y'all will do graphing a parabola by plotting a few points.
Graph ![]() .
.
Solution
We volition graph the equation by plotting points.
| Cull integers values for x, substitute them into the equation and solve for y. | ||
| Record the values of the ordered pairs in the chart. | 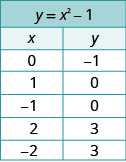 | |
| Plot the points, and then connect them with a smooth curve. The result will be the graph of the equation | 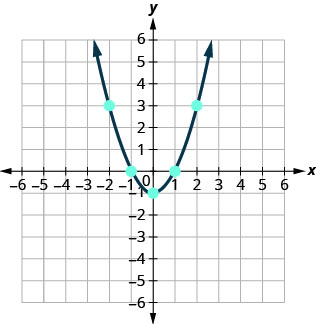 | |
Graph ![]() .
.
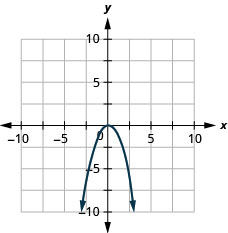
Graph ![]() .
.
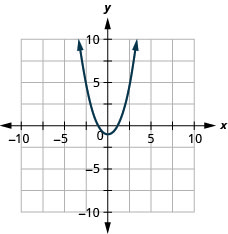
How do the equations ![]() and
and ![]() differ? What is the divergence between their graphs? How are their graphs the same?
differ? What is the divergence between their graphs? How are their graphs the same?
All parabolas of the form ![]() open upwards or downwards. See (Figure).
open upwards or downwards. See (Figure).
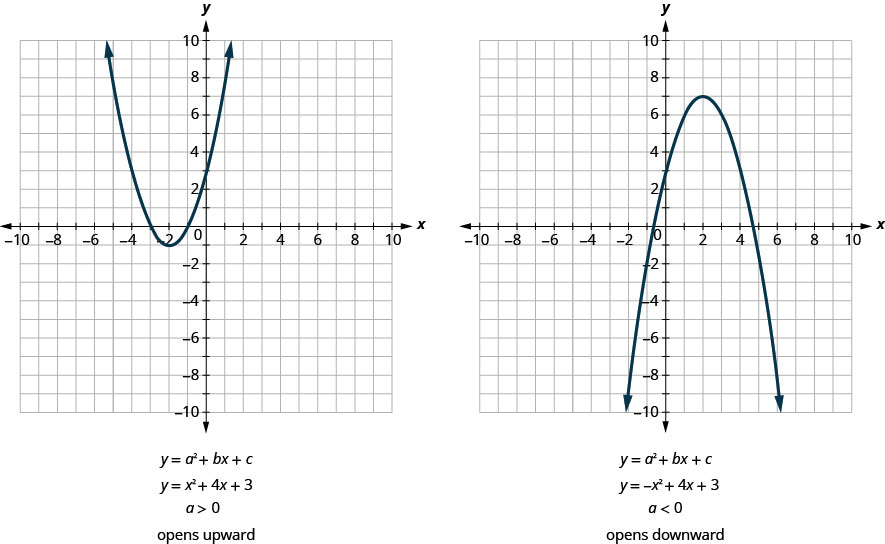
Notice that the only difference in the 2 equations is the negative sign before the ![]() in the equation of the 2d graph in (Figure). When the
in the equation of the 2d graph in (Figure). When the ![]() term is positive, the parabola opens upward, and when the
term is positive, the parabola opens upward, and when the ![]() term is negative, the parabola opens downward.
term is negative, the parabola opens downward.
Parabola Orientation
For the quadratic equation ![]() , if:
, if:

Determine whether each parabola opens upwardly or downward:
ⓐ ![]() ⓑ
ⓑ ![]()
Solution
| ⓐ Detect the value of "a". | 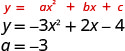 Since the "a" is negative, the parabola will open up downwards. | |
| ⓑ Find the value of "a". | 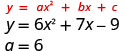 Since the "a" is positive, the parabola will open upward. | |
Decide whether each parabola opens upward or downward:
ⓐ ![]() ⓑ
ⓑ ![]()
ⓐ up ⓑ down
Determine whether each parabola opens up or downward:
ⓐ ![]() ⓑ
ⓑ ![]()
ⓐ down ⓑ up
Detect the Axis of Symmetry and Vertex of a Parabola
Look again at (Figure). Do you lot see that nosotros could fold each parabola in one-half and that ane side would lie on top of the other? The 'fold line' is a line of symmetry. We telephone call information technology the centrality of symmetry of the parabola.
Nosotros bear witness the same two graphs again with the axis of symmetry in cherry-red. Come across (Figure).
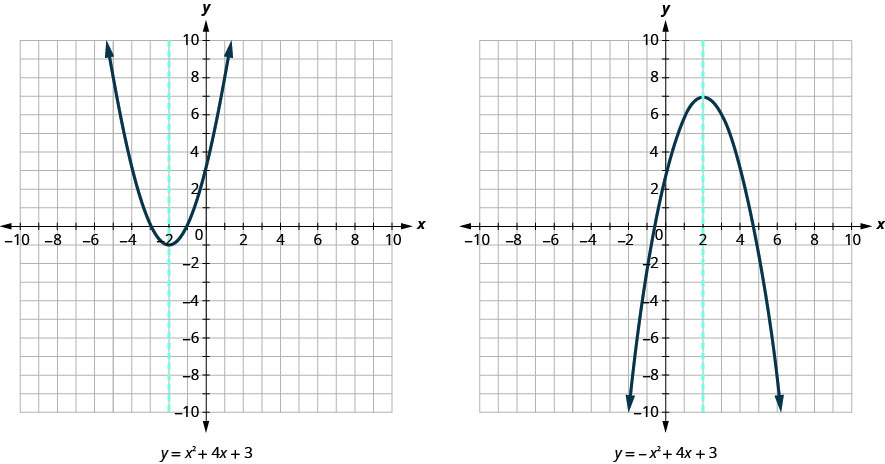
The equation of the axis of symmetry can be derived by using the Quadratic Formula. We volition omit the derivation here and continue directly to using the result. The equation of the centrality of symmetry of the graph of ![]() is
is ![]()
So, to find the equation of symmetry of each of the parabolas we graphed above, we will substitute into the formula ![]() .
.
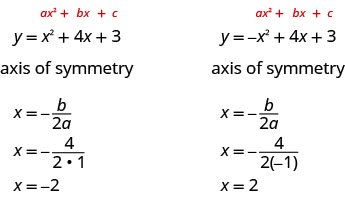
Await back at (Figure). Are these the equations of the dashed red lines?
The point on the parabola that is on the axis of symmetry is the everyman or highest point on the parabola, depending on whether the parabola opens up or downwards. This point is called the vertex of the parabola.
We can easily find the coordinates of the vertex, considering nosotros know it is on the axis of symmetry. This ways its 10-coordinate is ![]() . To find the y-coordinate of the vertex, nosotros substitute the value of the x-coordinate into the quadratic equation.
. To find the y-coordinate of the vertex, nosotros substitute the value of the x-coordinate into the quadratic equation.

Axis of Symmetry and Vertex of a Parabola
For a parabola with equation ![]() :
:
To observe the y-coordinate of the vertex, nosotros substitute ![]() into the quadratic equation.
into the quadratic equation.
For the parabola ![]() find: ⓐ the axis of symmetry and ⓑ the vertex.
find: ⓐ the axis of symmetry and ⓑ the vertex.
For the parabola ![]() find: ⓐ the axis of symmetry and ⓑ the vertex.
find: ⓐ the axis of symmetry and ⓑ the vertex.
ⓐ ![]() ⓑ
ⓑ ![]()
For the parabola ![]() notice: ⓐ the axis of symmetry and ⓑ the vertex.
notice: ⓐ the axis of symmetry and ⓑ the vertex.
ⓐ ![]() ⓑ
ⓑ ![]()
Find the Intercepts of a Parabola
When we graphed linear equations, nosotros often used the 10– and y-intercepts to assistance us graph the lines. Finding the coordinates of the intercepts will help united states of america to graph parabolas, too.
Remember, at the y-intercept the value of ![]() is zero. And so, to find the y-intercept, we substitute
is zero. And so, to find the y-intercept, we substitute ![]() into the equation.
into the equation.
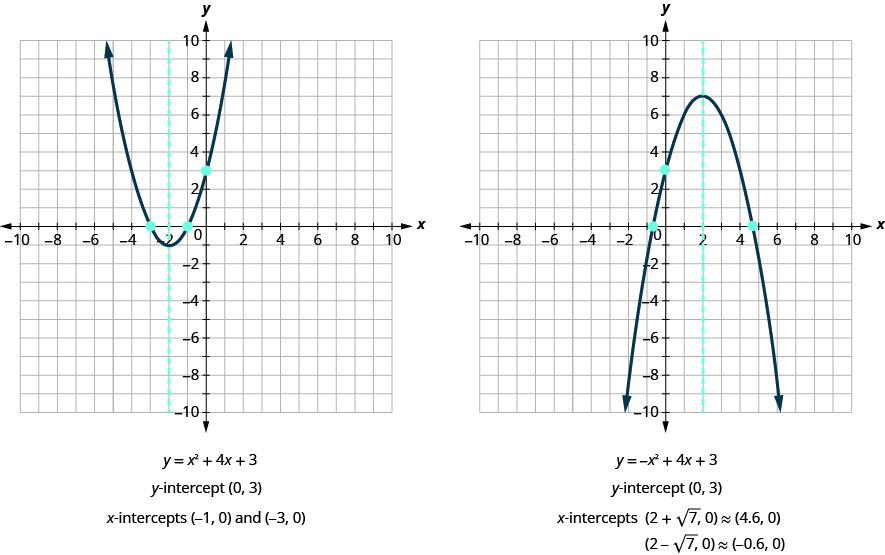
Let's notice the y-intercepts of the 2 parabolas shown in the effigy below.
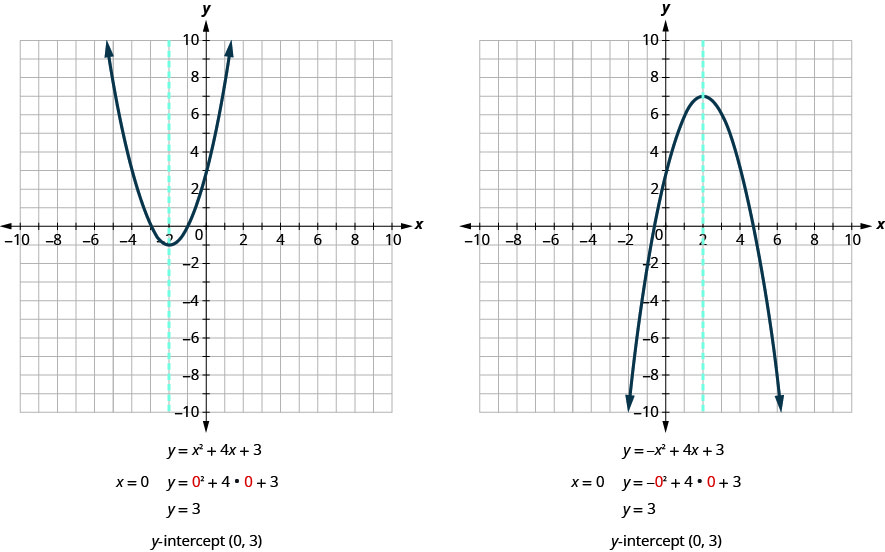
At an x-intercept, the value of ![]() is zero. To detect an ten-intercept, we substitute
is zero. To detect an ten-intercept, we substitute ![]() into the equation. In other words, we will demand to solve the equation
into the equation. In other words, we will demand to solve the equation ![]() for
for ![]() .
.
![]()
But solving quadratic equations like this is exactly what we have done before in this chapter.
Nosotros tin at present observe the 10-intercepts of the two parabolas shown in (Effigy).
First, we will notice the x-intercepts of a parabola with equation ![]() .
.
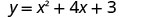 | ||
| Allow | 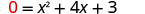 | |
| Cistron. | 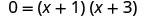 | |
| Use the zero product belongings. | 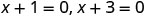 | |
| Solve. | 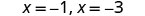 | |
| The x intercepts are | ||
Now, nosotros volition find the x-intercepts of the parabola with equation ![]() .
.
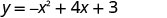 | ||
| Let | 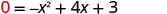 | |
| This quadratic does not factor, then we use the Quadratic Formula. | 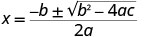 | |
| | 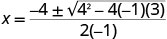 | |
| Simplify. | 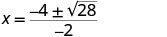 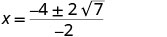 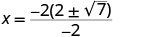 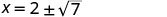 | |
| The x intercepts are | ||
Nosotros volition use the decimal approximations of the x-intercepts, so that nosotros can locate these points on the graph.
![]()
Practise these results agree with our graphs? See (Figure).
Find the intercepts of a parabola.
To observe the intercepts of a parabola with equation ![]() :
:
![]()
Find the intercepts of the parabola ![]() .
.
Discover the intercepts of the parabola ![]()
![]()
Find the intercepts of the parabola ![]()
![]()
In this chapter, nosotros take been solving quadratic equations of the form ![]() . We solved for
. We solved for ![]() and the results were the solutions to the equation.
and the results were the solutions to the equation.
We are at present looking at quadratic equations in two variables of the form ![]() . The graphs of these equations are parabolas. The x-intercepts of the parabolas occur where
. The graphs of these equations are parabolas. The x-intercepts of the parabolas occur where ![]() .
.
For example:

The solutions of the quadratic equation are the ![]() values of the 10-intercepts.
values of the 10-intercepts.
Earlier, we saw that quadratic equations take two, 1, or 0 solutions. The graphs below bear witness examples of parabolas for these three cases. Since the solutions of the equations give the x-intercepts of the graphs, the number of x-intercepts is the aforementioned as the number of solutions.
Previously, we used the discriminant to decide the number of solutions of a quadratic equation of the course ![]() . Now, we tin can use the discriminant to tell us how many x-intercepts there are on the graph.
. Now, we tin can use the discriminant to tell us how many x-intercepts there are on the graph.
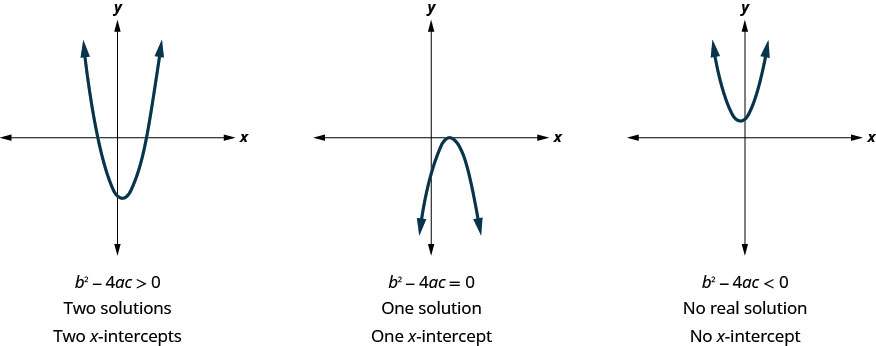
Before you get-go solving the quadratic equation to find the values of the x-intercepts, y'all may want to evaluate the discriminant and then you know how many solutions to wait.
Find the intercepts of the parabola ![]() .
.
Detect the intercepts of the parabola ![]()
![]()
Find the intercepts of the parabola ![]()
![]()
Find the intercepts of the parabola ![]() .
.
Find the intercepts of the parabola ![]()
![]()
Find the intercepts of the parabola ![]()
![]()
Graph Quadratic Equations in Two Variables
Now, we accept all the pieces we need in club to graph a quadratic equation in ii variables. We just need to put them together. In the side by side example, we will run across how to do this.
How To Graph a Quadratic Equation in Two Variables
Graph ![]() .
.
Graph the parabola ![]()
Graph the parabola ![]()
Graph a quadratic equation in two variables.
- Write the quadratic equation with
 on one side.
on one side. - Determine whether the parabola opens upward or downwardly.
- Find the axis of symmetry.
- Find the vertex.
- Find the y-intercept. Find the point symmetric to the y-intercept beyond the centrality of symmetry.
- Find the x-intercepts.
- Graph the parabola.
We were able to find the ten-intercepts in the last example by factoring. We find the x-intercepts in the next example by factoring, too.
Graph ![]() .
.
Graph the parabola ![]()
Graph the parabola ![]()
For the graph of ![]() , the vertex and the x-intercept were the same signal. Remember how the discriminant determines the number of solutions of a quadratic equation? The discriminant of the equation
, the vertex and the x-intercept were the same signal. Remember how the discriminant determines the number of solutions of a quadratic equation? The discriminant of the equation ![]() is 0, so there is just ane solution. That ways there is but ane 10-intercept, and it is the vertex of the parabola.
is 0, so there is just ane solution. That ways there is but ane 10-intercept, and it is the vertex of the parabola.
How many 10-intercepts would y'all await to see on the graph of ![]() ?
?
Graph ![]() .
.
Graph the parabola ![]()
Graph the parabola ![]()
Finding the y-intercept past substituting ![]() into the equation is piece of cake, isn't it? But we needed to employ the Quadratic Formula to find the x-intercepts in (Figure). We volition use the Quadratic Formula again in the next example.
into the equation is piece of cake, isn't it? But we needed to employ the Quadratic Formula to find the x-intercepts in (Figure). We volition use the Quadratic Formula again in the next example.
Graph ![]() .
.
Graph the parabola ![]()
Graph the parabola ![]()
Solve Maximum and Minimum Applications
Knowing that the vertex of a parabola is the everyman or highest indicate of the parabola gives us an like shooting fish in a barrel style to determine the minimum or maximum value of a quadratic equation. The y-coordinate of the vertex is the minimum y-value of a parabola that opens upward. It is the maximum y-value of a parabola that opens downwardly. See (Figure).
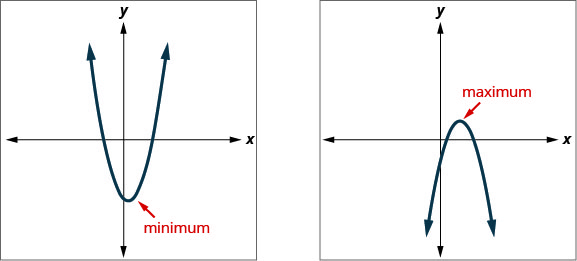
Minimum or Maximum Values of a Quadratic Equation
The y-coordinate of the vertex of the graph of a quadratic equation is the
- minimum value of the quadratic equation if the parabola opens upward.
- maximum value of the quadratic equation if the parabola opens downward.
Find the minimum value of the quadratic equation ![]() .
.
Find the maximum or minimum value of the quadratic equation ![]() .
.
The minimum value is ![]() when
when ![]() .
.
Notice the maximum or minimum value of the quadratic equation ![]() .
.
The maximum value is 5 when ![]() .
.
Nosotros accept used the formula
![]()
to summate the peak in feet, ![]() , of an object shot upwards into the air with initial velocity,
, of an object shot upwards into the air with initial velocity, ![]() , after
, after ![]() seconds.
seconds.
This formula is a quadratic equation in the variable ![]() , and so its graph is a parabola. By solving for the coordinates of the vertex, we can find how long information technology volition take the object to attain its maximum top. Then, nosotros can calculate the maximum acme.
, and so its graph is a parabola. By solving for the coordinates of the vertex, we can find how long information technology volition take the object to attain its maximum top. Then, nosotros can calculate the maximum acme.
The quadratic equation ![]() models the height of a volleyball hitting straight upwardly with velocity 176 anxiety per 2nd from a height of iv feet.
models the height of a volleyball hitting straight upwardly with velocity 176 anxiety per 2nd from a height of iv feet.
- ⓐ How many seconds will it take the volleyball to achieve its maximum superlative?
- ⓑ Find the maximum elevation of the volleyball.
Solution
![]()
Since a is negative, the parabola opens downward.
The quadratic equation has a maximum.
- ⓐ
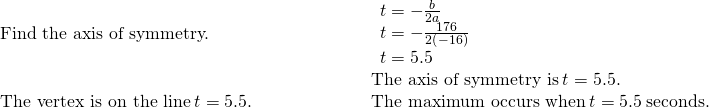
- ⓑ
Find h when 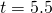 .
.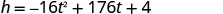
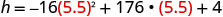
Use a calculator to simplify. 
The vertex is 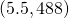 .
.Since the parabola has a maximum, the h-coordinate of the vertex is the maximum y-value of the quadratic equation. The maximum value of the quadratic is 488 feet and it occurs when 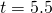 seconds.
seconds.
The quadratic equation ![]() is used to discover the height of a stone thrown upward from a meridian of 32 feet at a rate of 128 ft/sec. How long volition it take for the stone to reach its maximum pinnacle? What is the maximum tiptop? Round answers to the nearest tenth.
is used to discover the height of a stone thrown upward from a meridian of 32 feet at a rate of 128 ft/sec. How long volition it take for the stone to reach its maximum pinnacle? What is the maximum tiptop? Round answers to the nearest tenth.
It will take 4 seconds to reach the maximum height of 288 feet.
A toy rocket shot upward from the ground at a rate of 208 ft/sec has the quadratic equation of ![]() . When volition the rocket attain its maximum tiptop? What will exist the maximum height? Round answers to the nearest tenth.
. When volition the rocket attain its maximum tiptop? What will exist the maximum height? Round answers to the nearest tenth.
It volition take six.5 seconds to reach the maximum superlative of 676 feet.
Key Concepts
Department Exercises
Practice Makes Perfect
Recognize the Graph of a Quadratic Equation in Two Variables
In the following exercises, graph:
![]()
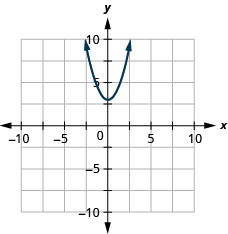
![]()
In the post-obit exercises, determine if the parabola opens upward or down.
![]()
downward
![]()
![]()
up
![]()
Notice the Axis of Symmetry and Vertex of a Parabola
In the following exercises, notice ⓐ the axis of symmetry and ⓑ the vertex.
![]()
![]()
Find the Intercepts of a Parabola
In the post-obit exercises, find the ten– and y-intercepts.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Graph Quadratic Equations in Two Variables
In the following exercises, graph by using intercepts, the vertex, and the axis of symmetry.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Solve Maximum and Minimum Applications
In the post-obit exercises, find the maximum or minimum value.
![]()
The minimum value is ![]() when
when ![]() .
.
![]()
![]()
The minimum value is half dozen when ![]() .
.
![]()
![]()
The maximum value is xvi when ![]() .
.
![]()
In the following exercises, solve. Round answers to the nearest tenth.
An pointer is shot vertically upward from a platform 45 anxiety high at a rate of 168 ft/sec. Apply the quadratic equation ![]() to find how long it will take the arrow to reach its maximum height, and and so find the maximum height.
to find how long it will take the arrow to reach its maximum height, and and so find the maximum height.
In 5.3 sec the pointer will attain maximum elevation of 486 ft.
A stone is thrown vertically upward from a platform that is 20 feet high at a rate of 160 ft/sec. Use the quadratic equation ![]() to detect how long it will take the rock to reach its maximum height, and then find the maximum height.
to detect how long it will take the rock to reach its maximum height, and then find the maximum height.
A rancher is going to fence three sides of a corral next to a river. He needs to maximize the corral surface area using 240 feet of fencing. The quadratic equation ![]() gives the surface area of the corral,
gives the surface area of the corral, ![]() , for the length,
, for the length, ![]() , of the corral along the river. Detect the length of the corral along the river that volition give the maximum area, and then find the maximum surface area of the corral.
, of the corral along the river. Detect the length of the corral along the river that volition give the maximum area, and then find the maximum surface area of the corral.
The length of the side along the river of the corral is 120 feet and the maximum area is 7,200 sq ft.
Everyday Math
Writing Exercises
For the revenue model in (Figure) and (Effigy), explain what the x-intercepts hateful to the computer shop owner.
Answers will vary.
For the acquirement model in (Effigy) and (Figure), explain what the x-intercepts hateful to the backpack retailer.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to better?
Chapter 10 Review Exercises
ten.3 Solve Quadratic Equations Using the Quadratic Formula
In the following exercises, solve by using the Quadratic Formula.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
no real solution
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In the following exercises, make up one's mind the number of solutions to each quadratic equation.
In the following exercises, identify the most advisable method (Factoring, Square Root, or Quadratic Formula) to utilize to solve each quadratic equation.
ⓐ gene ⓑ Quadratic Formula ⓒ foursquare root
10.4 Solve Applications Modeled by Quadratic Equations
In the post-obit exercises, solve by using methods of factoring, the square root principle, or the quadratic formula.
Find two sequent odd numbers whose product is 323.
Two consecutive odd numbers whose product is 323 are 17 and 19, and ![]() and
and ![]()
Find two consecutive even numbers whose production is 624.
A triangular banner has an area of 351 foursquare centimeters. The length of the base is 2 centimeters longer than four times the height. Observe the height and length of the base of operations.
The height of the banner is 13 cm and the length of the side is 54 cm.
Julius congenital a triangular display instance for his coin collection. The height of the display case is half-dozen inches less than twice the width of the base of operations. The area of the of the dorsum of the case is seventy square inches. Find the height and width of the case.
A tile mosaic in the shape of a correct triangle is used equally the corner of a rectangular pathway. The hypotenuse of the mosaic is five feet. One side of the mosaic is twice as long as the other side. What are the lengths of the sides? Round to the nearest tenth.

The lengths of the sides of the mosaic are 2.2 and 4.4 anxiety.
A rectangular piece of plywood has a diagonal which measures two feet more the width. The length of the plywood is twice the width. What is the length of the plywood's diagonal? Round to the nearest tenth.
The front walk from the street to Pam's house has an area of 250 square feet. Its length is 2 less than four times its width. Detect the length and width of the sidewalk. Round to the nearest tenth.
The width of the front end walk is eight.ane anxiety and its length is 30.eight feet.
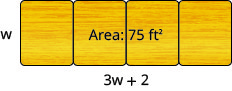
For Sophia'due south graduation party, several tables of the same width will be arranged end to finish to give a serving tabular array with a total area of 75 square feet. The full length of the tables will exist two more than than three times the width. Find the length and width of the serving table so Sophia can purchase the correct size tablecloth. Circular respond to the nearest 10th.
A ball is thrown vertically in the air with a velocity of 160 ft/sec. Use the formula ![]() to determine when the ball will exist 384 anxiety from the ground. Round to the nearest tenth.
to determine when the ball will exist 384 anxiety from the ground. Round to the nearest tenth.
The ball will achieve 384 feet on its style up in 4 seconds and on the way downwardly in half dozen seconds.
A bullet is fired straight up from the ground at a velocity of 320 ft/sec. Utilize the formula ![]() to decide when the bullet will reach 800 anxiety. Round to the nearest 10th.
to decide when the bullet will reach 800 anxiety. Round to the nearest 10th.
x.5 Graphing Quadratic Equations in Two Variables
In the post-obit exercises, graph by plotting point.
Graph ![]()
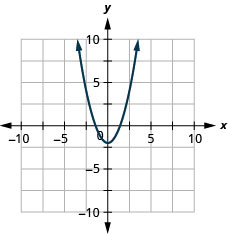
Graph ![]()
In the post-obit exercises, decide if the following parabolas open up up or down.
![]()
down
![]()
![]()
upward
![]()
In the following exercises, observe ⓐ the axis of symmetry and ⓑ the vertex.
![]()
In the following exercises, find the x– and y-intercepts.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In the following exercises, graph by using intercepts, the vertex, and the axis of symmetry.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In the following exercises, find the minimum or maximum value.
![]()
The minimum value is ![]() when
when ![]() .
.
![]()
In the following exercises, solve. Rounding answers to the nearest tenth.
A ball is thrown upward from the ground with an initial velocity of 112 ft/sec. Use the quadratic equation ![]() to find how long information technology will accept the ball to reach maximum height, and so observe the maximum pinnacle.
to find how long information technology will accept the ball to reach maximum height, and so observe the maximum pinnacle.
In 3.5 seconds the ball is at its maximum elevation of 196 feet.
Practice Exam
Use the Square Root Holding to solve the quadratic equation: ![]() .
.
![]()
Utilise Completing the Square to solve the quadratic equation: ![]() .
.
Use the Quadratic Formula to solve the quadratic equation: ![]() .
.
![]()
Solve the following quadratic equations. Utilise any method.
![]()
![]()
![]()
![]()
![]()
no real solution
![]()
Use the discriminant to determine the number of solutions of each quadratic equation.
![]()
2
![]()
Solve by factoring, the Square Root Property, or the Quadratic Formula.
Find two consecutive even numbers whose product is 360.
2 sequent even number are ![]() and
and ![]() and 18 and xx.
and 18 and xx.
The length of a diagonal of a rectangle is three more than than the width. The length of the rectangle is three times the width. Find the length of the diagonal. (Round to the nearest tenth.)
For each parabola, find ⓐ which means information technology opens, ⓑ the axis of symmetry, ⓒ the vertex, ⓓ the x– and y-intercepts, and ⓔ the maximum or minimum value.
![]()
![]()
Graph the following parabolas by using intercepts, the vertex, and the centrality of symmetry.
![]()
![]()
Solve.
A water airship is launched upwardly at the rate of 86 ft/sec. Using the formula ![]() , notice how long it will take the balloon to reach the maximum height and then detect the maximum height. Round to the nearest 10th.
, notice how long it will take the balloon to reach the maximum height and then detect the maximum height. Round to the nearest 10th.
Source: https://opentextbc.ca/elementaryalgebraopenstax/chapter/graphing-quadratic-equations/
Posted by: gillespieextesed.blogspot.com


0 Response to "How To Find X In Quadratic Equation"
Post a Comment